Oldřich Botlík: Slova, která by se měla tesat

Publikujeme text Oldřicha Botlíka ilustrující příčiny selhávání maturantů při řešení úlohy, která podle mnohých patří do matematiky na druhém stupni základní školy. V čem tyto příčiny vidí?

V souvislosti s jednotnými přijímacím zkouškami na střední školy se diskutovalo a diskutuje také o jejich dopadech na výuku. Následující příspěvek se objevil v diskusi pod jedním článkem na České škole (Kvaternion, 15. března 2017 16:29).

Deformace přijímačkami se projevuje tím, že učitelé drilují žáky a studenty na typových úlohách z přijímaček (a rodiče to po nich požadují), čímž se vytvářejí potěmkinovské poznatky. Žák je schopen vyřešit typovou úlohu, kterou rozpozná pomocí signálů v zadání, ale ve skutečnosti problematice vůbec nerozumí a není schopen poznatek nijak využít v jakékoli jiné situaci, tedy ani u méně standardní úlohy. Taková znalost je tedy fakticky jen kulisa, která se při pohledu z jedné strany – tedy skrze typovou úlohu – jeví jako skutečný poznatek, ale ve skutečnosti jím není, za kulisou je prázdno. Z hlediska (nejen) matematického vzdělání takový přístup nejenže naprosto není přínosný (čímž popírám tvrzení, že by – bez dalších podmínek – bylo pokrokem, kdyby žáci uměli alespoň to, co je v přijímačkových testech), ale je přímo škodlivý, protože předává žákům chybnou informaci o tom, co je matematika a jak se na ni připravovat. Na školy se dostávají cvičené opice, které dril přímo vyžadují a nejsou schopné ani ochotné samostatně myslet a zkoumat.
(nepatrně kráceno)

Už dlouho jsem nic tak výstižného nečetl, i když další průběh diskuse ukázal, že někteří její účastníci Kvaternionovo sdělení nechápou. Chci je proto ilustrovat jednou pěknou úlohou z loňského maturitního testu z matematiky a podrobnějším rozborem pozadí výsledků maturantů. Ukazuje se totiž, že příčiny jejich hromadného selhání mají kořeny někde hluboko v základním vzdělávání. Zdaleka však nejde jen o špatné zvládnutí jednoho vzorečku. Na neúspěšnosti má nemalý podíl také samotný přístup žáků k problému a jeho řešení.

Žáci, čerpadla a matematika
Nádrž se plní několika stejně výkonnými čerpadly. Dvě čerpadla by stejnou nádrž naplnila za x hodin (x je větší než 0). Vyjádřete v hodinách, za jak dlouho by stejnou nádrž naplnilo
n čerpadel (n je přirozené číslo).

Ačkoli panovala téměř jednoznačná shoda, že jde o učivo základní školy, a úloha byla v maturitním testu zařazena jako „rozjížděcí“, zvládlo ji jen necelých 16 % maturantů. Vysvětlení? Úloha nebyla standardní a signál (čerpadla) nevedl žáky tak, jak možná byli zvyklí. A to „učivo základní školy“? Se souhlasem organizátora projektu Kalibro zde uvádím výsledky podobné úlohy (dva kombajny sklidí lán pšenice za x hodin), ale snazší. Byla letos zařazena do matematického testu pro žáky ukončující základní vzdělávání. Žáci dostali nabídku osmi vztahů s hledaným počtem hodin H a měli za úkol vybrat VŠECHNY vztahy, které platí:

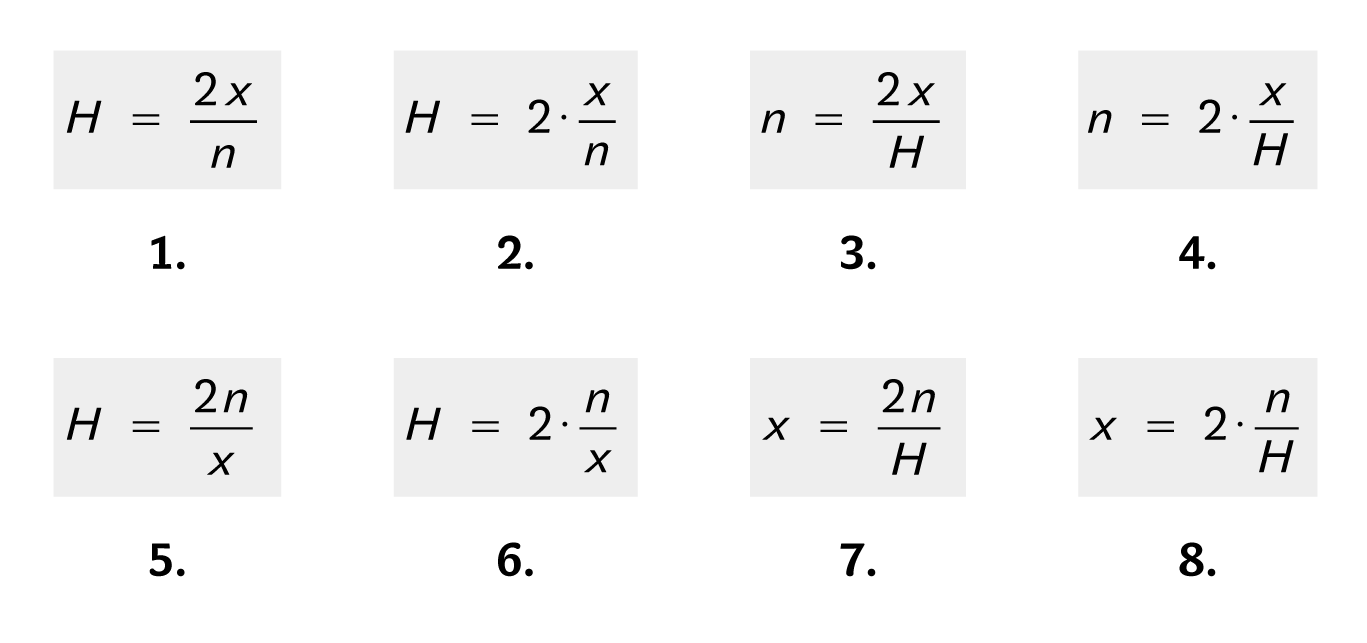
Při pozornějším pohledu je ihned zřejmé, že vztahy v horním řádku jsou ekvivalentní, vztahy v dolním také. Například rozdíl mezi vztahy 1 a 2 spočívá v tom, že dvěma se jednou násobí čitatel, podruhé celý zlomek. Rozdíl je tedy jen kosmetický. Přesto z žáků, kteří vybrali vztah 1, jen necelá pětina (17,9 %) vybrala také vztah 2. Mezi tím, kolik žáků vybíralo jednotlivé správné položky v horním řádku, nejsou velké rozdíly (maximálně 6 procentních bodů) – průměrně to bylo 32 % žáků. Ještě menší rozdíly (maximálně 2 procentní body) jsou mezi tím, kolik žáků vybíralo jednotlivé nesprávné položky v řádku dolním – průměrně to bylo 30 % žáků. Celkem 3 % žáků uvedla, že neplatí žádný nabízený vztah, 13 % žáků vynechalo úlohu úplně. Bez jediné chyby odpověděla pouhá 3 % žáků – to jsou ti, kteří vybrali všechny vztahy v horním řádku a žádné jiné. Výsledek dívek byl o 1 procentní bod lepší než výsledek chlapců.

Výrazná část žáků tedy zjevně jen tipovala, ale řádně vycvičené opice by jako celek dopadly lépe. Ty by – při opravdu náhodném tipování – musely dosáhnout průměrné úspěšnosti kolem 50 %, zatímco testovaní žáci dosáhli průměrné úspěšnosti pouhých 44 % (žáci získávali 12,5 procentních bodů, tedy jednu osminu ze sta, za každý správně posouzený vztah).

Dovednosti, které žáci nepoužili
Proč byla úloha s osmi nabízenými vztahy snazší než ta maturitní? Právě díky tomu, že žáci nemuseli vztah mezi proměnnými n, x, H vymýšlet sami. Mohli snadno vyloučit vztahy v dolním řádku. Jednou ze základních matematických dovedností je totiž v podobné situaci dosazení. Žáci ze zadání vědí, že pro n = 2 musí vyjít H = x. A konečně, nebylo vlastně ani moc obtížné ověřit, že třeba vztah 1 platí. Práce se singulární hodnotou (jedno čerpadlo) je druhou základní matematickou dovedností využitelnou v této úloze. Když dvěma čerpadlům trvá naplnění nádrže x hodin, jednomu čerpadlu to musí trvat 2x hodin. Když je čerpadel n, trvá jim to n-krát kratší dobu, tedy 2x/n.

Právě tohle vylučování a ověřování je současně důvodem, proč v maturitním testu nemají být zaškrtávací úlohy (s jediným řešením): vybrat správný vztah z hotové nabídky je PRINCIPIÁLNĚ JINÁ ÚLOHA než správný vztah sestavit. V reálném světě totiž člověk nabídku vztahů na výběr nejspíš nepotká. Ze zveřejněných maturitních výsledků není zřejmé, kolik procent maturantů sice nějaký vztah sestavilo, ten ale nebyl správný. Jejich autoři nezkontrolovali výsledek své práce, a proto nejméně v jedné z obou výše zmíněných dovedností selhali zcela jistě. Cermat má dokonce databázi všech vztahů, které maturanti sestavili, učitelé a didaktici matematiky ale do ní z nezná­mých důvodů nemají přístup.

Pro pořádek zbývá dodat, že data jsou za 2 424 žáků základních škol. Podobně jako u maturitního testu nešlo o náhodný výběr, výsledky jsou tudíž pouze ilustrativní. Přesto pomáhají objasnit, proč vlastně na úlohách „ze základní školy“ selhávají i maturanti.

Výsledky dávají Kvaternionovi za pravdu v tom, že významná část žáků si z výuky matematiky neodnáší základní dovednosti potřebné pro ověření platnosti jednoduchého vztahu. Na podstatě matematiky se přitom tyto dovednosti podílejí MNOHEM VÍC než vzoreček, o který šlo. Protože jsou univerzální, a matematiku dokonce daleko přesahují. Běžně se říká, že výuka matematiky rozvíjí myšlení žáků. Výsledky obou výše uvedených úloh však ukazují, že bez splnění dalších předpokladů to prostě není pravda.