← Beduin ← Články

Maturita z matematiky: při rozhodování o úspěchu a neúspěchu hrála vloni velkou roli náhoda

1. 6. 2020

EDUin

Co přinesl týden 25. 5. – 31. 5. 2020

Krátce:

Startují maturity a maturanti se modlí, aby něco nechytili. Bez horečky a s čestným prohlášením. Josef Mačí na Seznam.cz upozorňuje, že kvůli tomu nemusí odmaturovat část studentů, kteří trpí běžnou infekcí a ke zkoušce by za běžných okolností šli. Źe jde o reálný problém potvrdila karanténa 11 gymnazistů, jejichž spolužačka se nakazila koronavirem (idnes.cz). Ministerstvo školství nenabídlo žákům, kteří musí být v karanténě, jinou možnost, než složit maturitu na podzim (Česká televize), řešení nakonec našli místní hygienici (ČT).
Minulý týden odstartoval ministr školství Robert Plaga návrhem na částečný návrat žáků 2. stupně a středoškoláků do škol, který odpoledne přijala vláda (irozhlas.cz). Upravený harmonogram ministerstva školství pro otevření škol vzápětí okomentovaly školské asociace, v omezeném otevření škol pro starší žáky neviděly smysl. (irozhlas.cz) „Uvědomujeme si, že plný návrat druhého stupně není možný,“ řekl Plaga České televizi. Přesto alespoň částečné obnovení výuky podle něj má smysl. Ten je však více než vzdělávací spíše socializační, dodal také, že rozhodnutí je na školách.
Žáci 1. stupně mají za sebou první týden školy. Školy na něj byly podle texty na Aktualne.cz dobře připraveny, zájem dětí se lišil škola od školy. Někde se vrátilo pár dětí, jinde to bylo přes polovinu žáků. Ministra Plagu za jeho postup zkritizovala opozice. Lidovec Marek Výborný poukázal na to, že je vše na ředitelích (MF dnes), senátor Michael Canov označil dobrovolnou školní docházku za ústavní paskvil (idnes.cz). Piráti uprostřed týdne vydali svůj vlastní plán pro školství, ve kterém ministerstvo obvinili, že zmatkuje. Článek Josefa Mačího pak uprostřed týdne upozornil na paradox uzavřených skupin, po nichž se děti odpoledne promíchají na kroužcích (Seznam.cz). Ministerstvo pro další týdny toto pravidlo uvolnilo (Novinky.cz).
V Česku se s koronavirem přímo setkalo zhruba 500 dětí, po vyléčení se budou vracet do škol. „Máme zkušenost, že koronavirus ani nemuselo mít samotné dítě, stačilo, že bylo z rodiny, kde se nákaza vyskytla. A na malém městě už byl problém, že to dítě jde do školy. Objevují se tlaky na to, aby takové dítě do školy nešlo,“ říká předseda Asociace ředitelů základních škol. S obavami spojenými s návratem dětí, ať už nemocí COVID 19 onemocněly ony, nebo někdo v jejich okolí, se podle Černého setkávají zejména na menších školách. (irozhlas.cz)
Ministerstvo školství počítá pro příští rok s růstem učitelských platů, a to o již v minulém roce avizovaných 9 procent. „Závazek programového prohlášení vlády platí, a platný střednědobý výhled na rok 2021 tak navýšení platů pedagogických pracovníků o devět procent obsahuje, stejně tak jako navýšení platů nepedagogů,“ řekla mluvčí ministerstva Aneta Lednová (Lidovky.cz).

Výrok týdne: „Spravedlivý přístup vyžaduje více než jen individuální hodnocení pro všechny žáky. Vyžaduje existenci třídní komunity, do níž jsou zapojeni všichni žáci, i ti znevýhodnění, v níž se diskutuje, a úkoly se propojují s mimoškolním prostředím žáků. Žádný počítač nedokáže být vzorem pro dítě hledající příklady chování dospělých pro to, čím by se chtělo stát,” popisuje Bořivoj Brdička důležitost role učitele pro vytváření spravedlivého vzdělávacího prostředí při zavádění technologiemi podporované personifikace. (Spomocnik.cz)

V souvislostech:

MATURITA Z MATEMATIKY: PŘI ROZHODOVÁNÍ O ÚSPĚCHU A NEÚSPĚCHU HRÁLA VLONI VELKOU ROLI NÁHODA

Měření dovedností není triviální problém, a to platí i pro maturitní test z matematiky. Podívali jsme se s pomocí dat, která Cermat uvolnil na základě zákona o svobodném přístupu k informacím, jak se s ním vypořádal loňský maturitní test z matematiky.

Teorie odpovědi na položku (IRT, Item Response Theory) je soubor moderních statistických metod, které umožňují kvantifikovat schopnost žáka vyřešit zadaný testy na základě toho, jak maturant odpovídal na jednotlivé otázky. První pokus o přepočet odpovědí žáků na tuto schopnost ukázal velkou skupinu studentů, kteří měli podobný předpoklad v loňském testu z matematiky uspět, jen části z nich se to ale podařilo.

Jak velký je tento překryv, ukazuje graf. Na vertikální ose je zaznamenána vypočítaná schopnost maturantů. Čím širší jsou “housle”, tím více žáků schopnost dané úrovně prokázalo. Zeleně je označeno rozpětí mezi nejvyšší dovedností dosaženou neúspěšnými maturanty a nejnižší dovedností dosaženou maturanty, kteří v testu uspěli. Naznačuje, jak velký je počet žáků, o jejichž osudu rozhodlo bodování úloh v testu nebo rovnou náhoda.

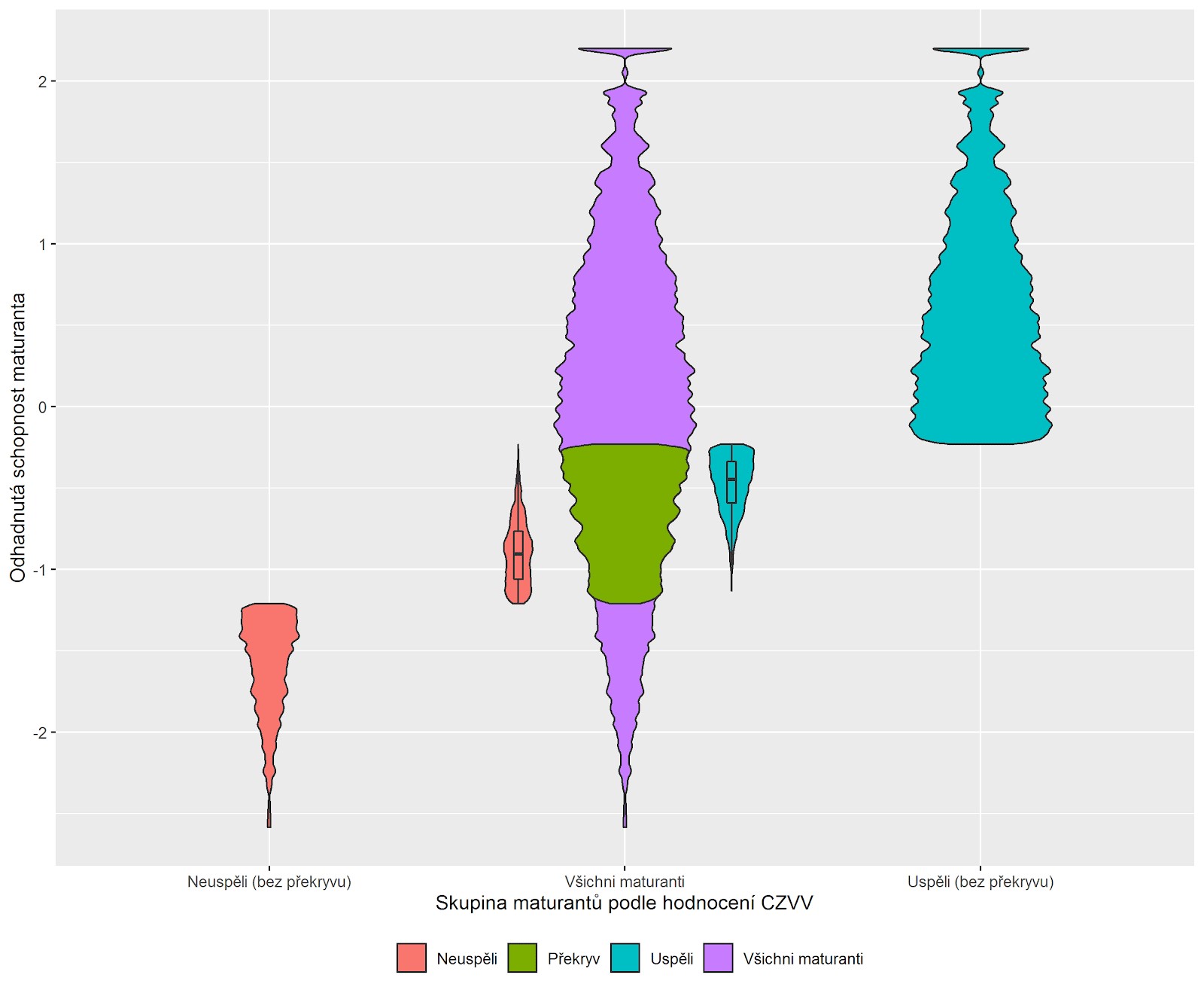
Jak velký vliv bude mít na konečný výsledek náhoda a způsob bodování záleží na řadě okolností. Vliv na to má například náročnost úloh, z nichž se test skládá. Dokonalý test by mohl být sestaven z perfektních úloh, u nichž by se dalo dopředu říci, že je například všichni žáci s úrovní schopnosti 2 vyřeší správně, zatímco žádný žák s úrovní dovednosti 1 ji nevyřeší. Tak to ale v reálném světě nefunguje. U jednoduché úlohy se možná dá předpokládat, že na ni skoro všichni dobří žáci odpovědí správně, s klesající dovedností bude stoupat podíl těch, kdo ji nevyřeší, až bude pravděpodobnost úspěchu podobně náhodná, jako by si žák hodil mincí. Až u nejhorších žáků bude zase očekávatelné, že úlohu skoro žádný z nich nevyřeší. Takové nahodilosti se samozřejmě žádný test nevyhne a může být informativní, ale pouze za předpokladu, že se s ní dobře statisticky pracuje.

Různě velkou roli hraje náhoda také při řešení různých typů úloh. Známým příkladem jsou uzavřené úlohy s nabídkou čtyř možných odpovědí. Ty dávají i žákovi, který nezná správnou odpověď, 25 % šanci. U takové úlohy může mít žák s nižší schopností větší šanci, než kdyby řešil stejně náročnou otevřenou úlohu. Jsou-li uzavřené úlohy ohodnoceny dvěma body a úlohy otevřené bodem jedním, může neurčitost v testu hrát větší roli, i pokud jsou uzavřené úlohy adekvátně obtížnější.

Ještě komplikovanější je to s úlohami, které umožňují získat body za částečný úspěch. Žák má například nalézt bod X a poté kolem něj sestrojit kružnici procházející body Y a Z. Jeden bod může získat za nalezení bodu X, druhý za sestrojení kružnice. Pokud měl u hledání bodu smůlu, platí za ni nakonec dvakrát a zůstane bez bodu.

Největší oříšek lze ale nalézt v jedné z úloh v testu z matematiky z roku 2019. Jedná se o úlohu, v níž má maturant ke každé ze čtyř rovnic o jedné neznámé přiřadit správnou odpověď ze šesti možností s tím, že počet bodů se řídí počtem správně přiřazených odpovědí. Představme si dva maturanty, každý z nich udělá v první odpovědi chybu – první vybere možnost, která nepatří k žádné z dalších rovnic. Druhý vybere výsledek, který ve skutečnosti patří k druhé rovnici. Pokud druhý maturant své rozhodnutí ještě nepřehodnotí, jeho chyba se u druhé rovnice zdvojí, protože správnou odpověď již “vyplýtval”. První maturant je oproti němu ve výhodě, protože udělal “správnou” chybu. Jak u takových úloh zdůvodnit, proč žák dostane za dvě správné odpovědi jeden bod a za tři správné odpovědi body dva?

Pro testologa, který by chtěl rozlišit dovednost žáka od náhody a do hodnocení zahrnout i obtížnost jednotlivých podúloh, je to malé modelovací peklo. Statistické nástroje pro práci s ním sice existují, ale jsou velice vzdálené metodám dosud reportovaným CZVV (Cermat) a rozhodně neobnášejí fixní obodování úloh bez dalšího odůvodnění. Je otázka, proč jsou takové typy úloh do maturitních testů zařazovány, případně proč nejsou hodnoceny adekvátní statistickou metodou. Odpověď na ni zatím nikdo neposkytl. Bez ní ovšem nelze vyloučit, že stavba maturitních testů je problematická a výpočet schopnosti žáka není dostatečně sofistikovaný.

Jiří Münich, datový analytik EDUin

Výběr z Edukalendáře: